Array programming

In computer science, array programming languages (also known as vector or multidimensional languages) generalize operations on scalars to apply transparently to vectors, matrices, and higher dimensional arrays.

Array programming primitives concisely express broad ideas about data manipulation. The level of conciseness can be dramatic in certain cases: it is not uncommon to find array programming language one-liners that require more than a couple of pages of Java code.^[1]

APL, designed by Ken Iverson, was the first programming language to provide array programming capabilities. The mnemonic APL refers to the title of his seminal book "A Programming Language" and not to arrays per se. Iverson's contribution to rigor and clarity was probably more important than the simple extension of dimensions to functions.

Concepts

The fundamental idea behind array programming is that operations apply at once to an entire set of values. This makes it a high-level programming model as it allows the programmer to think and operate on whole aggregates of data, without having to resort to explicit loops of individual scalar operations.

Iverson described^[2] the rationale behind array programming (actually referring to APL) as follows:

most programming languages are decidedly inferior to mathematical notation and are little used as tools of thought in ways that would be considered significant by, say, an applied mathematician. [...]

The thesis [...] is that the advantages of executability and universality found in programming languages can be effectively combined, in a single coherent language, with the advantages offered by mathematical notation. [...] it is important to distinguish the difficulty of describing and of learning a piece of notation from the difficulty of mastering its implications. For example, learning the rules for computing a matrix product is easy, but a mastery of its implications (such as its associativity, its distributivity over addition, and its ability to represent linear functions and geometric operations) is a different and much more difficult matter.

Indeed, the very suggestiveness of a notation may make it seem harder to learn because of the many properties it suggests for explorations.

[...]

Users of computers and programming languages are often concerned primarily with the efficiency of execution of algorithms, and might, therefore, summarily dismiss many of the algorithms presented here. Such dismissal would be short-sighted, since a clear statement of an algorithm can usually be used as a basis from which one may easily derive more efficient algorithm.

The basis behind array programming and thinking is to find and exploit the properties of data where individual elements are similar and/or adjacent. Unlike object orientation which implicitly breaks down data to its constituent parts (or scalar quantities), array orientation looks to group data and apply a uniform handling.

Function rank is an important concept to array programming languages in general, by analogy to tensor rank in mathematics: functions that operate on data may be classified by the number of dimensions they act on. Ordinary multiplication, for example, is a scalar ranked function because it operates on zero-dimensional data (individual numbers). The cross product operation is an example of a vector rank function because it operates on vectors, not scalars. Matrix multiplication is an example of a 2-rank function, because it operates on 2-dimensional objects (matrices). Collapse operators reduce the dimensionality of an input data array by one or more dimensions. For example, summing over elements collapses the input array by 1 dimension.

Uses

Array programming is very well suited to implicit parallelization; a topic of much research nowadays. Further, Intel and compatible CPUs developed and produced after 1997 contained various instruction set extensions, starting from MMX and continuing through SSSE3 and 3DNow!, which include rudimentary SIMD array capabilities. Array processing is distinct from parallel processing in that one physical processor performs operations on a group of items simultaneously while parallel processing aims to split a larger problem into smaller ones (MIMD) to be solved piecemeal by numerous processors. Processors with two or more cores are increasingly common today.

Languages

The canonical examples of array programming languages are APL, J, and Fortran 90. Others include: A+, IDL, K, Q, Mathematica, MATLAB, MOLSF, NumPy, GNU Octave, PDL, R, S-Lang, SAC, Nial and ZPL.

Examples

In scalar languages like FORTRAN 77, C, Pascal, etc. operations apply only to single values, so a+b expresses the addition of two numbers. In such languages adding two arrays requires indexing and looping:

Loop based approach

FORTRAN 77

00  DO 10 I = 1, N
        DO 10 J = 1, N
10         A(J,I) = A(J,I) + B(J,I)

C

for (i = 0; i < n; i++)
    for (j = 0; j < n; j++)
        a[i][j] += b[i][j];

C#

class Program
{
    static void Main(string[] args)
    {
        int[] numbers;                                         //Array declaration
 
        Console.WriteLine("Please enter the array size");
        int n = int.Parse(Console.ReadLine());                 //Getting the Array size from user
 
        numbers = new int[n];                                  //Array Creation
 
        for (int i = 0; i < numbers.Length; i++)               //Reading the Array Elements from user
        {
            Console.WriteLine("Enter number " + i + 1);
            numbers[i] = int.Parse(Console.ReadLine());
        }
    }
}

This need to loop and index to perform operations on arrays is both tedious and error prone.

In array languages, operations are generalized to apply to both scalars and arrays. Thus, a+b expresses the sum of two scalars if a and b are scalars, or the sum of two arrays if they are arrays. When applied to arrays, the operations act on corresponding elements as illustrated in the loops above.

Within the array programming paradigm, the previous C# code would become (e.g. in GNU Octave or in MATLAB languages):

numbers = sscanf( input( 'Enter numbers: ' , 's' ) , '%d ' )

without the need to statically decide the array size.

Array programming approach

Ada

The Ada language provides a library package^[3] supporting array-programming oriented syntax. Using that library, the example algorithm for adding element-by-element two matrices can be implemented as:

 with Ada.Numerics.Generic_Real_Arrays;
 
 A := A + B;

where A and B are two-dimensional arrays. It generates code that is effectively the same as the C loops shown above. An array language, therefore, simplifies programming but may come at a cost known as the abstraction penalty.^[4][5][6] Because the additions are performed in isolation to the rest of the coding, it may not produce the optimally most efficient code (for example if additions of other elements of the same array are subsequently encountered during the same execution, causing unnecessary repeated lookups). Even the most sophisticated optimizing compiler would have an extremely hard time amalgamating two or more apparently disparate functions which might appear in different program sections or sub-routines (yet this would be entirely obvious to a programmer who would naturally try to ensure the sums were aggregated on the same 'pass' of the array to minimize overhead).

Nial

The Nial array language allows an implementation with the same syntax^[7] used in the Ada example:

A := A + B

As another example, the following generates the inner product of two arrays (matrix multiplication):

a inner[+,*] b

Notice how the operations are sequenced on the arrays.

J

The J array language allows a pretty similar implementation of the basic example^[8]:

A =. A + B

However, the inner product of two arrays^[9] can be used to illustrate a typical right-to-left composition of operators (or "verbs") which is derived by the APL language:

+/ a * b

which can be read as "add" (+) "together" (/) the element-by-element product between a and b. The inner product can also been restated as a single composite^[10] operator (or "verb")

a (+/ . *) b

which can be read as "add together" (+/) "at" (. or also @:) the "element-by-element product" (*) between a and b.

MATLAB

A = A + B;

The implementation in MATLAB language allows the same economy allowed by using the Ada language. A variant of the MATLAB language is the GNU Octave language, which extends the original language also with augmented assignments so that the example can be implemented in the shortest way:

A += B;

Both MATLAB and GNU Octave natively support linear algebra operations such as matrix multiplication, matrix inversion, the numerical solution of system of linear equations even using the Moore–Penrose pseudoinverse.^[11][12] The Nial example of the inner product of two arrays can be implemented using the native matrix multiplication operator

a * b;

if a is a row vector of size [1 n] and b is a corresponding column vector of size [n 1]. The inner product between two matrices having the same number of elements can be implemented with the auxiliary operator (:) which efficiently reshape a given matrix to be a column vector, and the transpose operator ':

A(:)' * B(:);

An equivalent formulation of the "add together" and "element-by-element product" operators of J is in both MATLAB and GNU Octave languages the following

sum( A(:) .* B(:) );

where sum means "add together by columns" and .* means "element-by-element product". In this case, sum would add together the elements of a single column because of the use of the operator (:).

The solution of a system of n linear equations 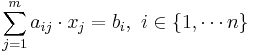expressed in matrix form A * x = b takes advantage of the native matrix left-division^[13] \:

x = A \ b;

which also automatically recognizes and works with both overdetermined and underdetermined systems using a pseudoinverse^[14] strategy to solve them.

R

 
  A = A + B;

The implementation in R language has a comprehensive suite of matrix operations. R natively supports linear algebra operations such as matrix multiplication, matrix inversion, the numerical solution of system of linear equations.

  a %*% b; # multiplication

The notation for the inner product of two matrices is compact:

   x <- 1:4
   x %*% x   # ''scalar ("inner") product (1 x 1 matrix)''

"Element-by-element" operations are

A * B
A + B

Additional matrix functionalities are available via packages such as OpenMx which e.g. supports lower/upper/Std matrices. Other packages support sparse-matrix operations as GNU Octave / MATLAB natively do.

However GNU R is unable to provide compact semantic notations such as native matrix left- of right-divisions. Solving a linear system would require to invoke a solve(.) function as in many other languages (or language libraries). This would not directly affect the conciseness:

   x <- solve( A , b )

is only twice the length of the corresponding GNU Octave /MATLAB notation and still extremely compact. The only feature which could be more difficult to preserve is the language ability to use the notation for deducing results by directly expressing and developing mathematical reasoning with the source code.

Mathematical reasoning and language notation

The matrix left-division operator concisely expresses some semantic properties of matrices. As in the scalar equivalent, if the (determinant of the) coefficient (matrix) A is not null then it is possible to solve the (vectorial) equation A * x = b by left-multiplying both sides by the inverse of A: A-1 (in both MATLAB and GNU Octave languages: A^-1). The following mathematical statements hold when A is a full rank square matrix:

A^-1 *(A * x) == A^-1 * (b)

(A^-1 * A)* x == A^-1 * b       (matrix-multiplication associativity)

x = A^-1 * b

where == is the equivalence relational operator. The previous statements are also valid MATLAB expressions if the third one is executed before the others (numerical comparisons may be false because of round-off errors).

If the system is overdetermined - so that A has more rows than columns - the pseudoinverse A+ (in MATLAB and GNU Octave languages: pinv(A)) can replace the inverse A-1, as follows:

pinv(A) *(A * x) == pinv(A) * (b)

(pinv(A) * A)* x == pinv(A) * b       (matrix-multiplication associativity)

x = pinv(A) * b

However, these solutions are neither the most concise ones (e.g. still remains the need to notationally differentiate overdetermined systems) nor the most computationally efficient. The latter point is easy to understand when considering again the scalar equivalent a * x = b, for which the solution x = a^-1 * b would require two operations instead of the more efficient x = b / a. The problem is that generally matrix multiplications are not commutative as the extension of the scalar solution to the matrix case would require:

(a * x)/ a == b / a

(x * a)/ a == b / a       (commutativity does not hold for matrices!)

x * (a / a) == b / a       (associativity also holds for matrices)

x = b / a

The MATLAB language introduces the left-division operator \ to maintain the essential part of the analogy with the scalar case, therefore simplifying the mathematical reasoning and preserving the conciseness:

A \ (A * x) == A \ b

(A \ A)* x == A \ b       (associativity also holds for matrices, commutativity is no more required)

x = A \ b

This is not only an example of terse array programming from the coding point of view but also from the computational efficiency perspective, which in several array programming languages benefits from quite efficient linear algebra libraries such as ATLAS or LAPACK.^[15][16]

Returning to the previous quotation of Iverson, the rationale behind it should now be evident:

it is important to distinguish the difficulty of describing and of learning a piece of notation from the difficulty of mastering its implications. For example, learning the rules for computing a matrix product is easy, but a mastery of its implications (such as its associativity, its distributivity over addition, and its ability to represent linear functions and geometric operations) is a different and much more difficult matter. Indeed, the very suggestiveness of a notation may make it seem harder to learn because of the many properties it suggests for explorations.

Third party libraries providing array-programming support to other languages

The use of specialized and efficient libraries to provide more terse abstractions is also common in other programming languages. In C++ several linear algebra libraries exploit the language ability to overload operators. It is interesting to notice that in some case a very terse abstraction in those languages is explicitly influenced by the array programming paradigm, as the Armadillo and Blitz++ libraries do.^[17][18]

Python

NumPy provides the nd-array object to the Python programming language. This provides much of the same functionality as Matlab.

See also

• Array slicing

References

External links

• "No stinking loops" programming
• Discovering Array Languages